لۆجیك و بیركاری!
ده‌ستپێك
واباوه له ناو خه‌ڵكدا كه كاتێك ووشه‌ی لۆجیك به‌كارده‌هێنت ئه‌وا مه‌به‌ستیان له‌وه‌یه كه ئاماژه به‌و ڕاستیه بكه‌ن كه شێوازی بیانووهێناوه‌كه‌یان دروسته و قسه‌كانیان هیچ شكو گومانێك هه‌ڵناگرێت، به‌لام له ڕاستیدا لۆجیك به كۆنترین به‌شی بیركاری داده‌نرێت به‌لكو له‌گه‌ڵیشیدا لۆجیك زۆرترین قورسایی له‌سه‌ر بناغه‌ی بیركاری داناوه، هه‌روه‌ك چۆن زۆرجاریش وا وێناكراوه كه لۆجیك بریتیه له سنوڕه لێڵاویه‌كه‌ی نێوان فه‌لسه‌فه و بیركاری.
لۆجیك بریتیه له لێكۆڵینه‌وه له حه‌قیقه‌ت وه ئایا چۆنیش ده‌كرێت حه‌قیقه‌تی یونیڤێرساڵ به‌ده‌ستبهێنرێت له‌ڕێگای هه‌ڵێنجانی بیركاریه‌وه. وه بنه‌ڕه‌تیترین به‌شی ئه‌و زمانه‌یه كه بیركاری پێی ده‌ئاخاوێت، هه‌روه‌ها لۆژیك ژێرخانی سه‌ره‌كی ڕێساكانی سه‌لماندنه.
لۆجیكی بیركاری و له‌گه‌لیشیدا هوونه‌ری بیانوهێنانه‌وه سه‌ره‌تاكه‌ی ده‌گه‌ڕێته‌وه بۆ چه‌ند هه‌زار ساڵێك له‌مه‌وبه‌ر، وه به‌تایبه‌تیش بۆ بیناسازه میسریه‌كان و فه‌له‌كناسه بابلیۆنه‌كان. دواتریش به جیا و به‌شێوه‌یه‌كی سه‌ربه‌خۆ له‌لایه‌ن چینیه‌كان و هیندیه‌كان گه‌شه‌ی پێكرا.
دوای زیاتر له چه‌ند سه‌ده‌یه‌ك، كۆمه‌لێكی زۆر و جیاواز له بیركاریزان و فه‌یله‌سوفه گریكه‌كان هاتن و گفتووگۆیان له‌سه‌ر سروشتی حه‌قیقه‌تیان كرد، وه هه‌وڵی ئه‌وه‌یاندا كه سیسته‌مێكی ره‌سمی ( فۆرماڵ) بۆ لۆجیك و هه‌ڵێنجاندن گه‌شه‌پێبده‌ن. ئایدیه‌كانی ئه‌فلاتۆن و ئه‌رستۆتالیس و هه‌ندێكی تریش تاوه‌كو سه‌ده‌كانی ناوه‌ڕاست بڕی كردو وه‌كو خۆی مانه‌وه، دواتر له‌سه‌ر ده‌ستی چه‌ند سكۆلارێكی وه‌كو سانت تۆماس ئاكوینس (Saint Thomas Aquinas) و هه‌ندێكی تر له بیركاریزانه عه‌ره‌به‌كان سه‌رله‌نوێ ژیایه‌وه.
گۆتفرید لیبینز (Gottfried Wilhelm Leibniz) ی ئه‌لمانی كه نه‌یاری ئیسحاق نیوه‌تن بوو به یه‌كێك بوو له‌و یه‌كه‌مین بیركاریزانانه داده‌نرێت كه به زمانی سیمبوڵ مامه‌ڵه‌ی له‌ته‌ك لۆژیكدا كرد، هه‌روه‌كو ئه‌وه‌ی كه ئێستا ئێمه به‌كاریده‌هێنین. له دوای ئه‌وه‌وه، لۆژیك به‌شێوه‌یه‌كی زۆر نزیك گرێدراوه به چه‌مكه‌كانی وه‌كو ئه‌كزیومه‌كانی سه‌لماندن و ناكۆتا و كۆمه‌ڵه‌ی ژماره‌كان.
كالكوله‌سی ڕێژه‌یی (Propositional Calculus)
زۆر نموونه‌مان هه‌یه له ده‌سته‌واژه و ڕسته‌ی بیركاری. بۆ نموونه 1+2=3 یاخود 4 ژماره‌یه‌كی جووته ئه‌م جۆره له ده‌سته‌واژانه زۆر ساده‌ن روون و ئاشكران كه ڕاستن، به‌لام ده‌سته‌واژه‌یه‌كی وه‌كو ژماره خۆبه‌شه‌كان جووتن هه‌ڵه‌یه. له لۆجیكدا ئێمه ( بیركاریزانه‌كان) به گشتی كه‌متر حه‌زمان به‌م جۆره ده‌سته‌واژانه‌ی سه‌ره‌وه هه‌یه به‌ڵكو ئه‌وه‌ی زیاتر له لۆجیكدا گرنگه كه ئاخۆ چۆن ده‌سته‌واژه‌كان پێكه‌وه ده‌توانین گرێ بده‌ین؟ سه‌ره‌تا ڕێگایه‌كی ئاسان هه‌یه بۆ ده‌ربڕینی هه‌ر ده‌سته‌واژه‌یه‌ك به پیته‌كانی وه‌كو P له‌گه‌ل Q. وه دواتریش ده‌بێت هه‌ریه‌ك له‌م ده‌سته‌واژانه یان گوزاره‌شتانه یان ده‌بێت راست بن T ( كه له True هاتوو به‌مانی ڕاستی) یاخود هه‌ڵه F (له False هاتووه به مانای هه‌ڵه) وه ناكرێت ده‌سته‌واژه‌یه‌ك له‌هه‌مانكاتدا هه‌م راست و هه‌میش هه‌ڵه‌بێت له هه‌مان كاتدا.
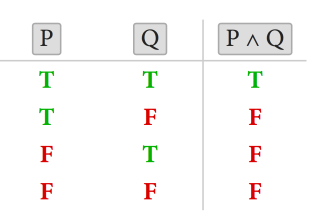
گه‌ر هاتوو دوو گوزاره‌شتی ( یان ده‌سته‌واژه‌ی) وه‌كو Q له‌گه‌ل P مان هه‌بوو ده‌توانین سێهه‌می لێ دروستبكه‌ین به‌م شێوه‌یه P ∧ Q كه مه‌به‌ست له‌و هێما بچووكه ∧ ئه‌وه‌یه كه ده‌سته‌واژه‌ی P ∧ Q ته‌نها و ته‌نها كاتێك راستده‌بێت گه‌ر هاتوو هه‌ریه‌كه له P وه Q ڕاست ببێت. ئه‌م په‌یوه‌ندیه‌ش ده‌كرێت له جه‌دوه‌لێكدا جێگا بكرێته‌وه كه به جه‌دوه‌لی راستی (truth table) ناسراوه له بیركاریدا. كاتێك بیر له‌سه‌رجه‌م ئه‌گه‌ره‌كان ده‌كه‌ینه‌وه بۆ P ∧ Q ئه‌وا ده‌بینین كه ته‌نها 4 ئه‌گه‌رمان هه‌یه. له خواره‌وه هه‌ر چوار ئه‌گه‌ره‌كه خراوه‌ته روو.
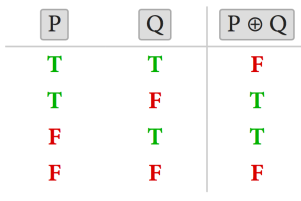
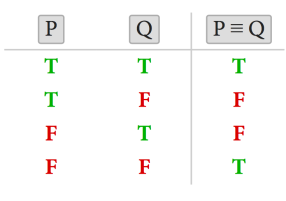
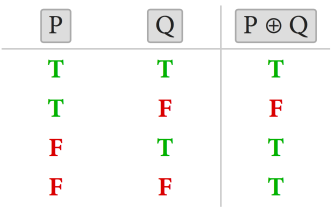
هه‌ندێكی تر له كرداره‌كان بریتیه له یه‌كسانبوونه كه ده‌توانرێت له‌گه‌ڵ گوزاره لۆجیكیه‌كاندا به‌كاربهێنرت به‌م جۆره P ≡ Q، وه ئه‌مه‌یش كاتێك ڕاستده‌بێت گه‌ر هاتوو هه‌ردوو كردارلێكراوه‌كان operands(لێره‌دا P وه Q) هه‌مان نرخیان هه‌بوو ( ده‌بێت هه‌ردووكیان ڕاستبن یاخود هه‌ردووكیان هه‌ڵه‌بن) جگه له‌مه‌یش كردارێكی تر بریتیه له یانی تایبه‌ت كه به‌م جۆره هێما ده‌كرێت P ⊕ Q، وه ئه‌مه‌یش كاتێك ڕاستده‌بێت گه‌ر هاتوو به‌لایه‌نی كه‌مه‌وه یه‌كێك له گوزاره‌كان ڕاست ، له خواره خشته‌ی ڕاستی هه‌ردوو كرداره‌كه خراوه‌ته ڕوو.
دواهه‌مین كرداریش بریتیه له implication ( به‌مانی P ده‌بێته هۆی ڕوودانی Q) كه به‌مشێوه‌یه هێمانده‌كرێت P 
Q. وه گوزاره‌ی هه‌ڵه له‌وانه‌یه ببێته هۆی هه‌ڵه یاخود ببێته هۆی ڕاست، واته پشت به گوزاره‌كه‌ی تر ده‌به‌ستێت، به‌لام گوزاره‌ی راست ته‌نها ده‌كرێت به‌هۆی گوزاره‌یه‌كی راستی تری وه‌كو Q بێت. سه‌رنجی ئه‌وه‌یش بده، ئه‌م كرداره جیاواز له دووكرداره‌كه‌ی سه‌ره‌وه هاوجێ نیه، واته كرداری implication هاوجێ نیه، ناتوانین جێگۆڕكێ به هه‌ردوو گوزاره‌ی P و Q بكه‌ین و ته‌سه‌وری ئه‌وه‌یش بكه‌ین هه‌مان ئه‌نجاممان ده‌ستبكه‌وێت.
ناشبێت ئه‌وه‌یشمان له‌بیربچێت كه ده‌كرێت نرخی گوزاره‌یه‌ك پێچه‌وانه بكه‌ینه‌وه ئه‌ویش له ڕێگه‌ی ئۆپه‌ره‌یته‌ری(كرداری) نه‌خێره‌وه كه به‌م جۆره هێما ده‌كرێت ¬. وه بۆ نموونه، گه‌ر هاتوو P ڕاست بوو ئه‌وا P¬ نه‌خێر ده‌بێت. گه‌ر هاتوو دووجار ئۆپه‌رێته‌ری نه‌خێرت دووباره كرده‌وه وه‌كو P = ¬¬P ئه‌وا ده‌كاته‌وه گوزاره‌كه خۆی .
پاشئه‌وه‌ی چه‌ند جۆرێك له ئۆپه‌رێته‌ری لۆجیكیمان پێناسه‌كرد، كاتی ئه‌وه هاتووه پێكه‌وه به‌كاریانبهێنین، واته
A ∧ (B ∨ C) ده‌كرێت له‌ڕێگه‌ی تێكه‌لكردنیان پێكه‌وه ده‌سته‌واژه‌ی زۆر ئاڵۆزمان ده‌ستبكه‌وێت. بۆ نموونه
كاتێك ڕاسته گه‌ر هاتوو A ڕاست بێت و به‌لایه‌نی كه‌مه‌وه‌وه یه‌كێك له B وه C یش ڕاستبێت. وه گه‌ریش سه‌رنجت دابێت ده‌بینیت كه كه‌وانه‌مان به‌كارهێناوه ئه‌وه‌یش له‌به‌ر ئه‌وه‌ی نه‌مانوویستووه بكه‌وینه ناو حاڵه‌تێكه‌وه كه زیاتر له نرخێكمان بۆ ده‌سته‌واژه‌كه‌ی سه‌ره‌وه ده‌ستبكه‌وێت، چونكه بێ هه‌بوونی كه‌وانه بوار ده‌كرێته‌وه بۆ ئه‌وه‌ی كه زیاتر له لێكدانه‌وه‌یه‌ك هه‌ڵبگرێت.
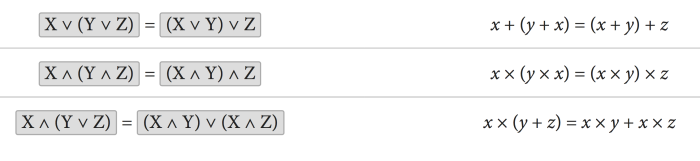
ئێمه هه‌ر له قۆناغه‌كانی بنه‌ڕه‌تیه‌وه ئاشنایه‌تیمان هه‌یه له‌گه‌ل ئۆپه‌رێته‌ره بیركاریه‌كان( كرداره بیركاریه‌كان) ی وه‌كو +, –, × له‌گه‌ل ÷ ئه‌م كرداره بیركاریانه له‌سه‌ر ژماره ئه‌نجامده‌درێت واته تۆ دێیت و دوو ژماره كۆده‌كه‌یته‌وه یاخود دابه‌شیان ده‌كه‌یت به‌م شێوه‌یه هه‌مان شتیش ده‌كرێت بۆ ده‌سته‌واژه لۆجیكیه‌كان بكه‌ین، به‌لام هه‌ڵبه‌ت له جیاتی كۆكردنه‌وه ∨ هه‌یه وه له‌به‌رامبه‌ر لێكدان ∧ مان هه‌یه. به‌لام ئۆپه‌رێته‌ره لۆجیكیه‌كان كه‌مێك نوێیه بۆمان وه ئه‌مانیش جۆرێك له جه‌بریه‌تی تایبه‌ت به خۆیان هه‌یه، وه به‌تایبه‌تیش پێی ده‌وترێت جه‌بری بۆڵیه‌ن (Boolean algebra) كه دیاره بۆڵیه‌ن بیركاریزانێكی به‌ریتانیه له‌نێوان ساڵه‌كانی (1815 – 1864) دا ژیاوه.
زۆرێك له رێساكانی ئه‌ریسماتیك وه‌ڕگێڕداران بۆ بۆڵیه‌ن ئه‌لجه‌برا وه‌كو ئه‌وه‌ی له خواره‌وه ده‌یبینین.
پیاوچاك و پیاوخراپ
ده‌كرێت لۆجیك و خشته‌ی ڕاستی به‌كاربهێنرێت بۆ شیكاركردنی زۆرێك له پرسیاره‌كانی ناو په‌زڵه‌كان، زۆرێك له‌و په‌زڵه به‌ناوبانگانه له‌لایه‌ن نووسه‌ری ئینگلیزی لویس كارۆله‌وه Lewis Ca
rroll (1832 – 1898) خراوه‌ته به‌تایبه‌تیش له‌ناو ڕۆمانی Alice in Wonderland كه كراوه به فیلمێكی سینه‌مائیش.
دوو نموونه له‌سه‌ر په‌زڵه لۆجیكیه‌كانی لویس كاڕۆل:-
ده‌ریاوانێك كاتێك كه‌شتیه‌كه‌ی نغرۆ ده‌بێت شه‌پۆله‌كانی ئاو ده‌ریاوانه‌كه ده‌باته كیشوه‌رێكی ته‌لیسماوی كه دوو ده‌سته خه‌لكی تیادا ده‌ژی، یه‌كێكیان ته‌نها ڕاستی ده‌لێن كه پیاوچاكن، وه تاقمه‌كه‌ی تر پیاوخراپن و ته‌نها درۆ ده‌ڵێن. وه دیاریشه كه ئه‌م دوو تاقه‌م پێكه‌وه ده‌ژین واته لێكجیاناكرێنه‌وه. ده‌ریاوانه‌كه ده‌یه‌وێت بگه‌ڕێته‌وه وه‌لاتی خۆی بۆیه ده‌چێت له ده‌رگای یه‌كێك له كوخه‌كان ئه‌دات. كاتێك پیاوی ماڵه‌كه ده‌رگاكه ده‌كاته‌وه به ده‌ریاوانه‌كه ڕاده‌گه‌یه‌نێت كه خۆی و ژنه‌كه‌ی پیاوخراپن. باشه ده‌ریاوانه‌كه پرسیار له كامیان بكات تاوه‌كو ڕێگای راستی ماڵه‌وه‌ی لێبپرسێت؟ ئه‌م پرسیاره ئاسانه گه‌ر هاتوو لۆجیك و خشته‌ی ڕاستیمان به‌كارهێنا. گریمان دوو گوزاره‌مان هه‌یه ئه‌وانیش H وه W وه دیاره ئه‌م دوو گوزاره‌یه كاتێك ڕاستده‌بێت گه‌رهاتوو پیاوه‌كه یاخود ژنه‌كه پیاو چاكبن به‌شێوه‌ی یه‌كله‌دوای یه‌ك، وه هه‌ڵه‌ده‌بێت گه‌ر هاتوو هه‌ردووكیان پیاوچاكبن. كاتێك پیاوه‌كه ده‌ڵێت هه‌ردووكیان پیاوخراپن واته H ∧ ¬W¬ . گه‌ر هاتوو پیاوه‌كه پیاوچاكبێت ئه‌وا ئه‌م گوزاره‌یه راستده‌بێت، وه گه‌ریشهاتوو پیاوخراپبێت ئه‌وا هه‌ڵه‌ده‌بێت، وه به‌تایبه‌تیش ئێمه ده‌زانین كه مه‌رجه H ≡ ¬H ∧ ¬W ڕاستبێت.
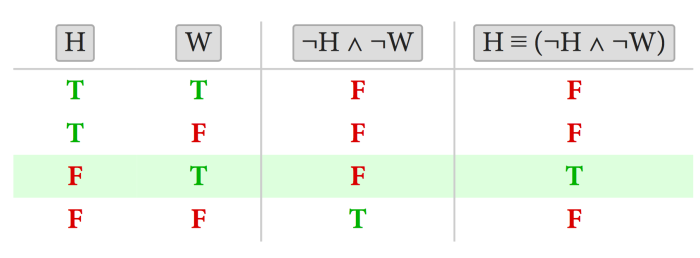
وه ده‌توانین له‌ڕێگه‌ی خشته‌ی ڕاستیه‌وه نرخی ئه‌م گوزاره‌یه دیاری بكه‌ین كه دیاره ئه‌مه پشت ده‌به‌ستێت به نرخی هه‌ریه‌ك له H وه W.
گه‌ر سه‌رنج له خشته‌ی ڕاستییه‌كه‌ی سه‌ره‌وه بده‌یت ده‌بینیت ته‌نها ڕیزێك كه نرخی له H ≡ ¬H ∧ ¬W راستبێت ده‌كاته ریزی سێهه‌م وه ئه‌وانی تر هه‌موویان هه‌ڵه‌ن. واته ڕیزی سێهه‌م كه پیاوه‌كه درۆزنه وه ژنه‌كه‌یش پیاوچاكه. كه‌واته ده‌ریاوانه‌كه پێیوسته پرسیار له ژنه‌كه بكات تاوه‌كو ئاراسته‌ی ڕاستی ماڵه‌وه‌یانی پێبڵێت.
له‌وانه‌یه یه‌كێك پرسیاری ئه‌وه بكات كه ده‌كرێت بێ خشته‌ی ڕاستیش وه‌لامی پرسیاری ده‌ریاوانه بزربووكه شیكاربكات. به‌لام زۆر پرسیاری ئالۆزتر هه‌یه كه زه‌حمه‌ته بێ خشته‌ی ڕاستی بتوانیت په‌زڵه‌كه شیكاربكه‌یت وه‌كو ئه‌وه‌ی خواره‌وه:
ده‌ریاوانه‌كه سێ كه‌سی دورگه‌كه‌ی بینی، بۆ ئاسانی كه‌سه‌كان به A,B,C بانگده‌كه‌ین. A ده‌ڵێت كه B وه C هه‌ردووكیان پیاوچاكن، وه B ده‌ڵێت كه A پیاوخراپه به‌لام C پیاوچاكه. ئێستا ده‌توانین پێمانبڵێیت كه كێ ڕاست ده‌بێژێت؟
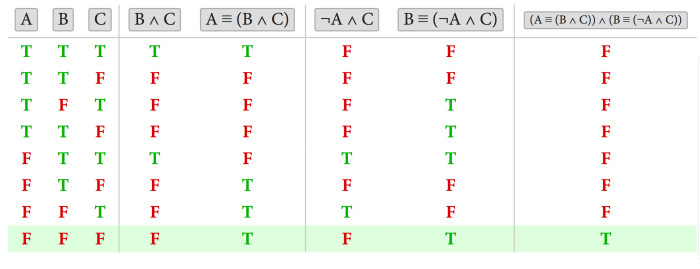
له‌به‌رئه‌وه‌ی كه له‌م په‌زله كه‌سێكی تر زیادی كردووه ئه‌مه‌یش واده‌كات كه له خشته‌ی ڕاستی سێ ڕیزی تر زیادببێت، به‌لام جۆری ئیشكردنه‌كه به‌هه‌مان شێوه‌ی پێشووتره. له‌م نموونه‌ی به‌رده‌ستمان ده‌بێت بزانین كه ئاخۆ ((A ≡ (B ∧ C)) ∧ (B ≡ (¬A ∧ C) كه ڕاستده‌بێت؟ وه پرسیار بۆ تۆ ئه‌وه‌یه كه كاربكه‌یت تاوه‌كو بزانیت كه چۆن ئه‌مه په‌یوه‌ندی به گوزاره سه‌ره‌كیه‌كه‌ی پێشووتره‌وه هه‌یه.
گه‌ر له خشته‌كه‌ی سه‌ره‌وه بده‌یت ئه‌وا ده‌بینیت كه ته‌نها ئه‌گه‌رێك بۆ ئه‌وه‌ی وه‌لامی ڕاستمان هه‌بێت ده‌بێت هه‌رسێ A,B,C پیاوخراپ بن چونكه ته‌نها دوا ریز ده‌بێته هۆی ئه‌وه‌ی كه ئه‌و ده‌سته‌واژه‌یه‌ی كه مه‌به‌ستمانه ڕاست بێت، كه دیاره ئه‌مه‌یش به‌داخه‌وه وا ده‌كات مه‌له‌وانه وونبووه‌كه باوه‌ر به وه‌لامی هیچكامیان نه‌كات.
چی له‌وه باشتر هه‌یه كه به ئه‌فلام كارتۆنێك كۆتایی به‌م بابه‌ته بهێنیتن، له‌گه‌ڵمبه….
دوا نموونه‌یش له‌سه‌ر ئه‌مه ئه‌فلام كارتۆنی سامورای جاكه (Samurai Jack ) له زنجیره‌یه‌كدا به‌ناوی حكایه‌تی جاكه، سامورای جاك بۆ گه‌یشتن به زه‌وی ئه‌فسووناوی پێویستی به‌وه هه‌یه كه پرسیار له ئه‌ژدیهایه‌كی دووسه‌ر بكات بۆ ئه‌وه‌ی ڕێگای راستی پیشانبدات، سه‌رێكی ئه‌ژدیهاكه ته‌نها قسه‌ی راست ده‌كات و سه‌ره‌كه‌ی تری ئه‌ژدیهاكه هه‌میشه قسه‌ی دروو ده‌كات، جاك پێویسته ته‌نها یه‌ك پرسیار بكات وه به‌و پرسیاره وه‌لامی راستی ده‌ستبكه‌وێت، ئایا ئه‌و پرسیاره چیه، فه‌رموو خۆت ئه‌و به‌شه‌ی جاك و ئه‌ژدیها دووسه‌ره‌كه ببینه!
http://world.mathigon.org/Logic_and_Paradoxes
سه‌رچاوه ماڵپه‌ڕی خوێندگه
خوێندنه‌وه‌ی ته‌واوی بابه‌ته‌كه
Reviewed by Unknown
on
7:05:00 ص
Rating:
مدون من بلد المليون و نصف شهيد احب مطالعة جديد العلوم و التقنيات مؤسس لمدونة علوم و تقنيات
ليست هناك تعليقات: